Profu de mate - Spot the math errors!

Spot the math errors!

3/11/2009 5:00:00 PM de la SkullsInTheStars.com

The first is:

2equals1

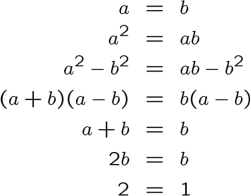
The second one is:

piequals3

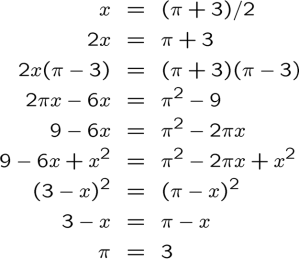
The third one is:

neg1equals1

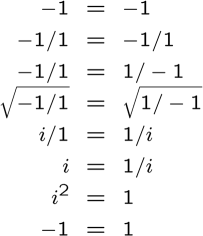
Each of these proofs is (intentionally) wrong! They highlight classic fallacies in mathematical thinking. See if you can figure out where, in each of them, the proof goes wrong, and then look for the answers below the fold…

(Note: the third proof involves the ‘imaginary number’ $i = \sqrt{-1}$ . If you’re not familiar with it, you can safely skip that problem, as it is closely related to one of the others.)

The mistake in the first proof is highlighted in red below:

2equals1error

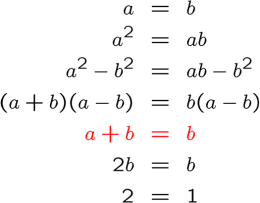
The mistake lies in the assumption that we can divide by $(a-b)$ . Why is this a problem? Because, according to the equation we started with, $a-b=0$ ! We are not allowed to divide by zero, and therefore the result highlighted in red is invalid.

The algebra ‘muddies the waters’ significantly, and it can be helpful to see the same proof, but with $a=b=1$ . The first two steps suggest that $1=1$ . The third step suggests that $1-1=1-1$ . The fourth step suggests that $2\cdot 0 = 1\cdot 0$ . We run into problems in the next step, in trying to divide both sides of this equation by zero!

The next ‘proof’ is a little more subtle. Again, we highlight the problem step in red:

piequals3error

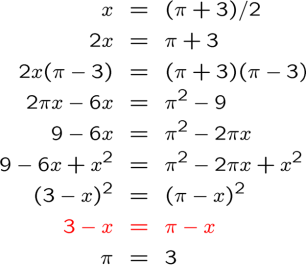
The problem here is that, in order to get to the step in red, there is an implicit square root taken of both sides of the equation. However, there are potentially two roots to any square; e.g. $x^2 = 9$ has possible solutions $x= +3$ or $x=-3$ . The ‘proof’ above assumes that the positive root is correct, which leads to the erroneous answer $\pi =3$ . If one looks at the negative root, one finds that $3-x = x-\pi$ , which leads right back to the starting equation $x = (\pi+3)/2$ . This proof, incidentally, might have been helpful to legislators in Indiana back in the late 1800s.

The third ‘proof’ suffers from essentially the same problem as the second, except that complex numbers are involved:

neg1equals1error

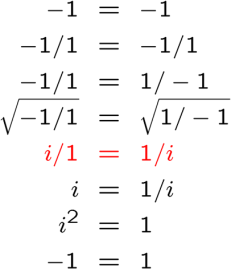
The step highlighted in red assumes that we break up the square roots as $\sqrt{-1/1}=\sqrt{-1}/\sqrt{1}$ , and then take individually the positive root of each term. It is wrong, however, to assume that the positive roots are always the correct ones when dealing with the square root of an equation. If we have an equation of the form

$a^2=c^2$ ,

we can at best say that $a=\pm c$ , and not necessarily both are true. Nothing changes if we take the square root of an equation of the form

$a^2/b^2=c^2/d^2$ ,

in which case we can at best conclude that

$a/b=\pm c/d$ .

For our ‘proof’ above, we find that the statement in red should be replaced with “ $i/1 = 1/i$ or $i/1 = -1/i$ , but not necessarily both.”

There’s a nice classic book that covers such mathematical errors, and other more important mathematical paradoxes: Bryan Bunch, Mathematical Fallacies and Paradoxes (Dover, New York, 1997).

If you really want to be certain that you understand such mistakes, try writing your own ‘proof’ for $100=0$ !Feel free to post yours in the comments. I’ll add my own ‘proof’ at a later date!

Spot the math errors!

Anunturi recomandate

cele mai noi materiale

reclame